«СЕМЬ ОСНОВНЫХ ИНСТРУМЕНТОВ КОНТРОЛЯ КАЧЕСТВА»
Контрольная карта
Контрольная карта (от англ. control chart) – это инструмент, позволяющий отслеживать ход протекания процесса во времени и при выявлении отклонений от предъявляемых к процессу требований воздействовать на него.
Впервые контрольные карты были предложены в 1924 году американским учёным, видным деятелем в области качества Уолтером Шухартом (1891–1967) в целях снижения изменчивости (вариабельности) процессов путём исключения отклонений, вызываемых несистемными причинами.
Все другие инструменты из числа «семи основных инструментов контроля качества», а именно: контрольный листок, диаграмма Парето, диаграмма Исикавы, гистограмма, диаграмма рассеяния и стратификация, дают возможность зафиксировать состояние процесса в определенный момент времени. В отличие от них контрольные карты позволяют отслеживать состояние процесса во времени и при необходимости воздействовать на него, причём прежде, чем процесс выйдет из-под контроля [1, с. 158; 2, с. 131].
Контрольные карты – самый важный инструмент статистического контроля качества. Каору Исикава (1915–1989), прославленный деятель в области управления качеством и один из творцов «японского экономического чуда», говорил: «Контроль качества начинается с контрольной карты и завершается ею» [2, с. 131].
С методикой контрольных карт предлагаем ознакомиться по учебному пособию «Управление качеством продукции» С.В. Пономарева, С.В. Мищенко, B.Я. Белобрагина и др. [3, с. 123–138]:
3.7. Контрольные карты процессов и временные ряды
3.7.1. Понятие о временном ряде
Временные ряды [44] применяются, когда требуется самым простым способом представить ход изменения наблюдаемых данных за определенный промежуток времени.
Временнóй ряд предназначен для наглядного представления данных, он очень прост в построении и использовании. Точки наносятся на график в том порядке, в каком они были собраны. Поскольку они отображают изменение характеристики во времени, очень существенна последовательность данных.
Одно из наиболее эффективных применений временного ряда заключается в выявлении существенных тенденций или изменений как мгновенных (индивидуальных), так и средних значений величины, характеризующей качество продукции. Пример построения временного ряда представлен на примере анализа сбыта (за 2000-2001 гг.).
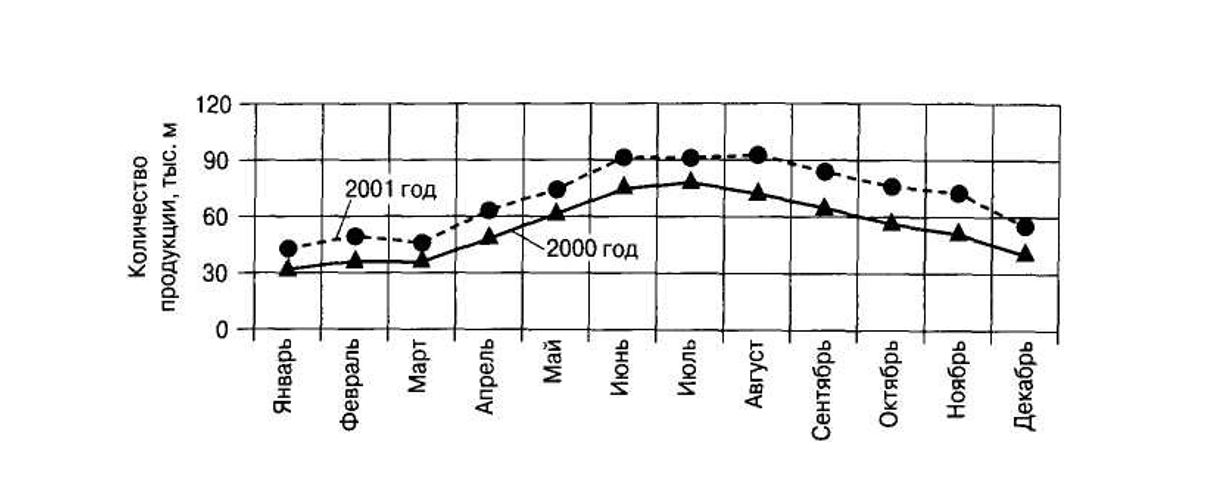
__________ 2000 г.; _ _ _ _ _ _ _ _ 2001 г.
Временные ряды могут быть очень полезны [44] при интерпретации и анализе статистических данных. Рассмотрим один из интересных случаев, иллюстрирующих успешное применение временных рядов [44].
В табл. 3.5 приведены статистические данные, описывающие протекание трех процессов.
Статистические данные, описывающие протекание трех процессов
| № п.п. |
Про- цесс № 1 |
Про- цесс № 2 |
Про- цесс № 3 |
№ п.п. |
Про- цесс № 1 |
Про- цесс № 2 |
Про- цесс № 3 |
|
|---|---|---|---|---|---|---|---|---|
| 1 | 35 | 32 | 29 | 27 | 39 | 40 | 35 | |
| 2 | 41 | 34 | 29 | 28 | 37 | 38 | 35 | |
| 3 | 39 | 30 | 30 | 29 | 39 | 39 | 36 | |
| 4 | 35 | 35 | 30 | 30 | 41 | 36 | 36 | |
| 5 | 30 | 31 | 30 | 31 | 34 | 41 | 36 | |
| 6 | 36 | 34 | 30 | 32 | 33 | 41 | 36 | |
| 7 | 36 | 29 | 30 | 33 | 37 | 37 | 37 | |
| 8 | 30 | 30 | 30 | 34 | 30 | 39 | 37 | |
| 9 | 35 | 29 | 31 | 35 | 35 | 37 | 37 | |
| 10 | 31 | 35 | 31 | 36 | 34 | 37 | 37 | |
| 11 | 31 | 30 | 31 | 37 | 39 | 39 | 37 | |
| 12 | 29 | 33 | 31 | 38 | 40 | 40 | 38 | |
| 13 | 33 | 33 | 32 | 39 | 38 | 40 | 38 | |
| 14 | 35 | 30 | 32 | 40 | 36 | 36 | 39 | |
| 15 | 40 | 32 | 33 | 41 | 37 | 37 | 39 | |
| 16 | 30 | 31 | 33 | 42 | 31 | 39 | 39 | |
| 17 | 37 | 33 | 33 | 43 | 40 | 35 | 39 | |
| 18 | 33 | 33 | 33 | 44 | 30 | 37 | 39 | |
| 19 | 34 | 31 | 33 | 45 | 36 | 41 | 40 | |
| 20 | 38 | 34 | 34 | 46 | 31 | 35 | 40 | |
| 21 | 33 | 31 | 34 | 47 | 32 | 36 | 40 | |
| 22 | 33 | 33 | 34 | 48 | 39 | 39 | 41 | |
| 23 | 30 | 34 | 34 | 49 | 29 | 38 | 41 | |
| 24 | 34 | 30 | 35 | 50 | 37 | 35 | 41 | |
| 25 | 41 | 30 | 35 | x | 34,9 | 34,9 | 34,9 | |
| 26 | 32 | 36 | 35 | Sn | 3,59 | 3,59 | 3,59 |
В нижней части табл. 3.5 представлены рассчитанные значения:
- средних арифметических значений x = 34,9;
- среднеквадратичных отклонений Sn = 3,59.
Видно, что средние арифметические значения и среднеквадратичные отклонения для всех трех процессов совпадают. В этом случае напрашивается вывод, что все три процесса можно считать одинаковыми. Многие начинающие исследователи, не имеющие опыта работы со статистическими методами обработки данных, сделали бы именно такой вывод. Однако так ли это на самом деле?
Временные ряды позволяют получить наиболее убедительный ответ на вопрос: «Являются ли три процесса, представленные в табл. 3.5 и имеющие одни и те же значения характеристик x = 34,9 (и S = 3,59), одинаковыми?» Для этого статистические данные следует представить в виде временных рядов, приведенных на рис. 3.10.
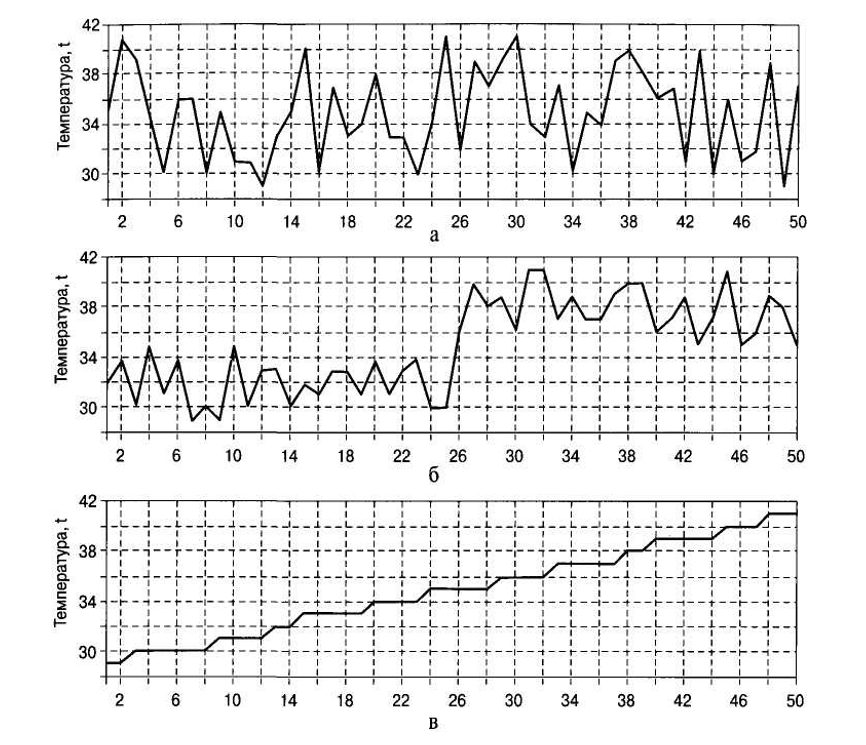
На рис. 3.10а видно, что процесс №1 является случайным процессом, который может быть охарактеризован средним арифметическим значением x = 34,9 и среднеквадратичным отклонением Sn = 3,59.
Временной ряд, изображенный на рис. 3.10б, позволяет сделать вывод о том, что процесс №2 имеет значительно меньший разброс данных (по сравнению с процессом №1) как на протяжении первой (Sn = 1,84), так и второй (Sn = 1,92) своей половины протекания. На рис. 3.10б видно, что на 25–27-м шагах было осуществлено вмешательство в ход процесса №2. В результате перенастройки процесса №2, первоначально характеризовавшегося средним арифметическим значением x = 31,9 и среднеквадратичным отклонением Sn = 1,84, параметры этого процесса изменились и приобрели значения x = 37,9 и Sn = 1,92.
Процесс №3 представляет собой (см. рис. 3.10в) пример закономерно возрастающего изменения характеристики процесса (так называемого тренда). Этот процесс имеет относительно небольшой случайный разброс, причем для него лучше не указывать какие-либо среднее арифметическое значение и среднеквадратичное отклонение (значения x = 34,9 и Sn = 3,59, приведенные в нижней части четвертого столбца табл. 3.5, не имеют реального физического смысла).
3.7.2. Понятие о контрольных картах
Контрольные карты [1, 8–10, 30–45] – это представление полученных в ходе технологического процесса данных в виде точек (или графика) в порядке их поступления во времени. Они позволяют контролировать текущие рабочие характеристики процесса, показывают отклонения этих характеристик от целевого или среднего значения, а также уровень статистической стабильности (устойчивости, управляемости) процесса в течение определенного времени. Их можно использовать для изучения возможностей процесса, чтобы помочь определить достижимые цели качества и выявить изменения средних характеристик и изменчивость процесса, которые требуют корректирующих или предупреждающих действий.
Контрольные карты впервые были предложены в 1924 г. У. Шухартом с намерением исключить необычные вариации, т.е. отделять вариации, которые обусловлены определенными причинами, от тех, что вызваны случайными причинами.
Контрольные карты основываются на четырех положениях [1, 8–10, 15, 30–45]:
- все процессы с течением времени отклоняются от заданных характеристик;
- небольшие отклонения отдельных точек являются непрогнозируемыми;
- стабильный процесс изменяется случайным образом, но так, что группы точек этого процесса имеют тенденцию находиться в прогнозируемых границах;
- нестабильный процесс отклоняется в силу неслучайных факторов, и неслучайными обычно считаются те отклонения, которые находятся за пределами прогнозируемых границ.
Контрольные карты позволяют использовать текущие данные процесса, чтобы установить статистически нормальные рабочие границы (границы регулирования), в которых должны находиться характеристики процесса.
Постоянное использование контрольной карты может помочь определить факторы, вызывающие отклонения процесса от заданных требований, и исключить их влияние.
Результаты измерений характеристики процесса в течение определенного времени сравниваются с требованиями к процессу для установления того, что контролируемая характеристика процесса [1, 8–10, 30, 38–45]:
- выходит за установленные границы поля допуска, но размах R (разброс параметров) процесса не превышает ширины поля допуска, что сохраняет возможность удовлетворить требования потребителя путем наладки или настройки процесса, например, за счет совмещения среднего арифметического значения x характеристики процесса с серединой поля допуска CL;
- выходит за установленные границы поля допуска, причем среднее значение x близко к середине поля допуска CL, а размах R (разброс параметров) процесса превышает ширину поля допуска, что не позволяет удовлетворить требования потребителя (необходимо улучшение процесса, а именно: уменьшение размаха R за счет использования более точного станка или уменьшения влияния внешних факторов, вызывающих повышенную изменчивость процесса);
- среднее значение x характеристики процесса далеко от середины поля допуска CL и величина размаха R превышает ширину поля допуска (для улучшения качества процесса требуется как его настройка/наладка, так и уменьшение размаха (разброса) характеристики процесса).
При разработке контрольной карты самым важным является способ определения контрольных границ. Для этого необходимо собрать большое количество данных (называемых предварительными данными), характеризующих состояние процесса, и на их основе рассчитать (по установленным формулам) контрольные границы. В производственной практике используются различные виды контрольных карт, отличающиеся друг от друга характером используемых данных.
Существуют два класса контрольных карт: один – для непрерывных значений, а второй – для дискретных. Сведения об основных типах контрольных карт [1, 8, 33, 37–43, 45] приведены в табл. 3.6.
Таблица 3.6
Основные типы контрольных карт
| Значения характеристики (показателя качества) |
Название |
|---|---|
| Непрерывные значения | х-карта (индивидуальных значений хi, карта измеряемых значений) (x–S)-карта (средних значений x и среднеквадратичных отклонений S) (x–R)-карта (средних значений x и размахов R) (x˜–R)-карта (медиан x˜ и размахов R) (x˜–S)-карта (медиан x˜ и среднеквадратичных отклонений S) |
| Дискретные значения | р-карта (для контроля доли несоответствующих (дефектных) изделий в подгруппе) nр-карта (для контроля числа несоответствующих (дефектных) изделий в подгруппе определенного объема n) с-карта (для контроля числа несоответствий (дефектов) в подгруппе) u-карта (для контроля числа несоответствий (дефектов), приходящихся на единицу продукции в подгруппе) |
Приведенная в табл. 3.6 классификация контрольных карт требует некоторых пояснений.
Контрольная карта индивидуальных (измеряемых) значений (х-карта) строится следующим образом (рис. 3.11).
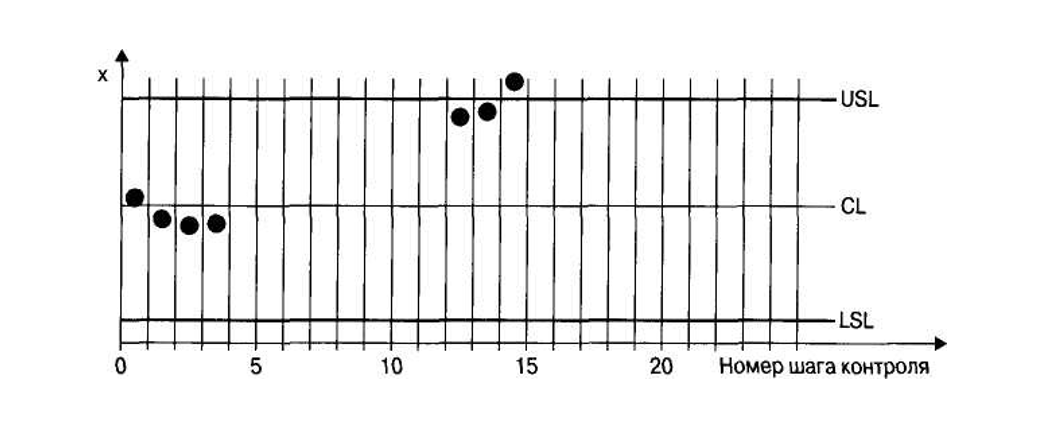
Через определенный промежуток времени (на очередном шаге контроля) рабочий снимает с конвейера по одной детали, измеряет значение х их характеристики качества и на бланке контрольной карты точками (крестиками, кружочками или другими значками) отмечает значение этой характеристики (см. рис. 3.11).
Если эти значки группируются вблизи середины х = CL поля допуска и не выходят за пределы верхней USL и нижней LSL границ поля допуска, то это означает, что процесс протекает в управляемых условиях. Если же на каком-либо шаге контроля эти значки приблизятся или даже выйдут за пределы поля допуска (см. шаги №13, 14, 15 на рис. 3.11), то это означает, что оператор должен вмешаться в ход процесса (произвести подстройку процесса, заменить износившийся инструмент и т.п.).
Опыт практической работы с х-картами показал, что они не всегда удобны в работе. Поэтому вместо карт индивидуальных значений (х-карт) чаще используют (x–S)-, (x–R)-, (x˜–R)-карты; (x˜–S)-карты на практике используются очень редко.
Рассмотрим обозначения х, S, x˜, R, использованные в табл. 3.6. Они имеют следующий смысл:
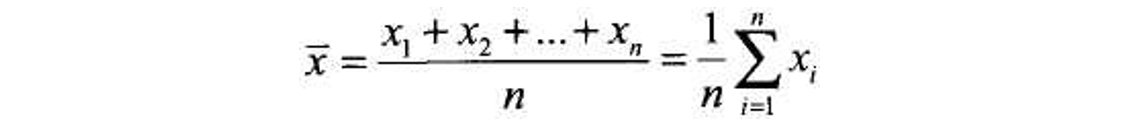
– среднеарифметическое значение характеристик качества х1, х2, ..., хn, измеренных рабочим на очередном шаге контроля;
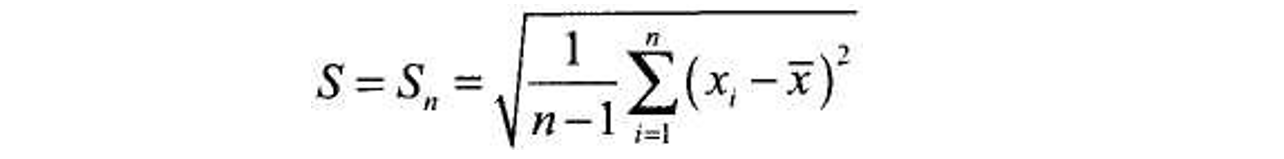
– среднеквадратичное отклонение характеристик качества х1, х2, ..., хn, измеренных рабочим на очередном шаге контроля.
В современных условиях контроля производственных процессов (с использованием компьютеров) вычисление среднего арифметического x и среднеквадратичного отклонения S не вызывает затруднений. Однако при внедрении контрольных карт на японских заводах в 50-е гг. XX в. компьютеров, пригодных для контроля производственных процессов, еще не было.
Поэтому вместо среднего арифметического значения x удобнее было использовать так называемую медиану x˜, значение которой определяется намного проще (без каких-либо вычислений). Если полученные при измерениях значения х1, х2, ..., хn характеристики качества расположить в возрастающем или убывающем порядке, то при нечетном числе измерений n медианой будет значение, занимающее срединное положение в этом ряду. При четном числе n медиана x˜ будет равна среднему арифметическому двух значений, расположенных в середине ряда.
При использовании медианы x˜ вместо среднего арифметического значения x целесообразно производить нечетное количество измерений.
Аналогично вместо среднеквадратичного отклонения S = Sn оказалось удобнее использовать так называемый размах R = хmах − xmin, т.е. разность между наибольшим хmах и наименьшим xmin значениями из ряда наблюдений х1, х2, ..., хn, выполненных на очередном шаге контроля. Правомерность замены среднеквадратичного отклонения S = Sn размахом R обоснована в работе [30] результатами расчета теоретического коэффициента корреляции между R и S, который оказался равен 0,977. Поэтому при использовании статистических методов управления качеством рассеивание процесса можно контролировать с помощью R-карты вместо S-карты.
Сведения о np-, p-, c- и u-картах приведены в правой части табл. 3.6 и в специальной литературе [1, 8, 38, 45].
3.7.3. Основные этапы построения контрольных карт
Рассмотрим этапы построения контрольной карты на примере (x–R)-карты. Эта карта используется для анализа и управления процессами, показатели качества которых представляют собой непрерывные величины (длина, вес, концентрация) и несут наибольшее количество информации о процессе. Величина x – есть среднее арифметическое значение для подгруппы, a R – выборочный размах для той же подгруппы. Обычно R-карту используют (вместе с x-картой) для контроля и управления разбросом (размахом) внутри подгруппы.
Перед практическим использованием (x–R)-карты необходимо подготовить бумажный бланк (или графические формы для отображения контрольной карты на экране компьютера), на котором эта контрольная карта будет изображаться (рис. 3.12). Для этого надо собрать данные о качестве протекания процесса и обработать их так, как это рассмотрено ниже [1, 8, 38, 45].
Сбор данных.
Пример результатов сбора исходных данных для построения контрольной карты типа (x–R) приведен в табл. 3.7.
Таблица 3.7
Данные для подготовки к построению (x–R)-карты [45]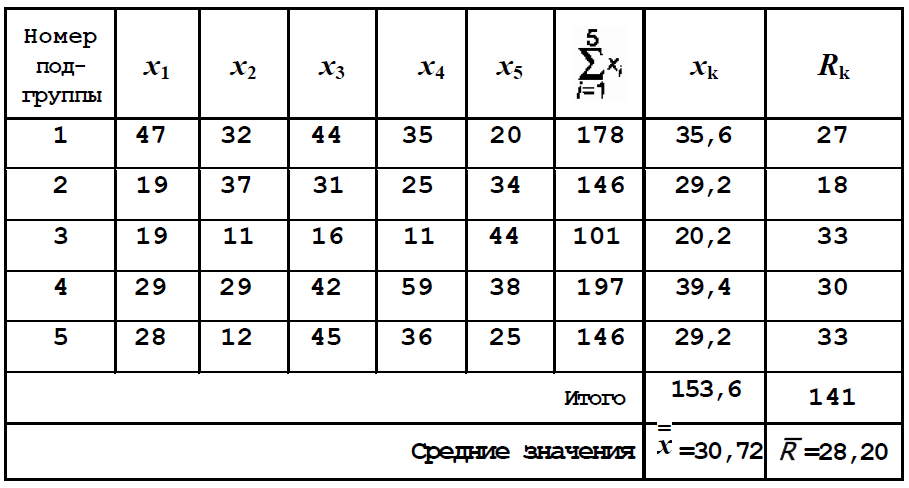
- Вычисление средних арифметических значений xk для каждой k-й подгруппы наблюдаемых значений:
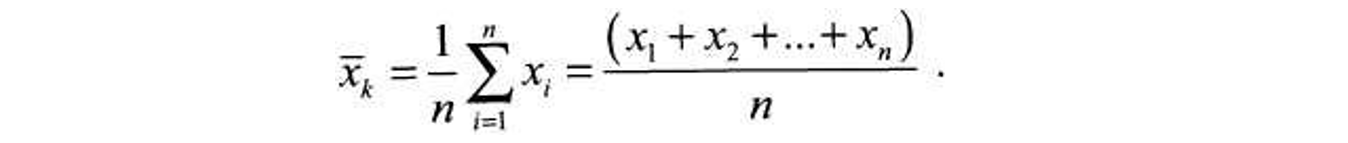
Результат xk обычно подсчитывается с одним лишним десятичным знаком по сравнению с исходными данными х1, х2, ..., хn.
Примечания:
- Для получения этих данных рабочий периодически (например, раз в час или после изготовления определенного количества деталей) снимает с производственного потока n деталей, измеряет их размеры х1, х2, ..., хn и для каждой подгруппы вычисляет среднее значение xk.
- Приведенные в табл. 3.7 данные содержат по пять значений в каждой подгруппе, что соответствует n = 5.
- Вычисление общего среднего значения x по всем имеющимся подгруппам данных по формуле:
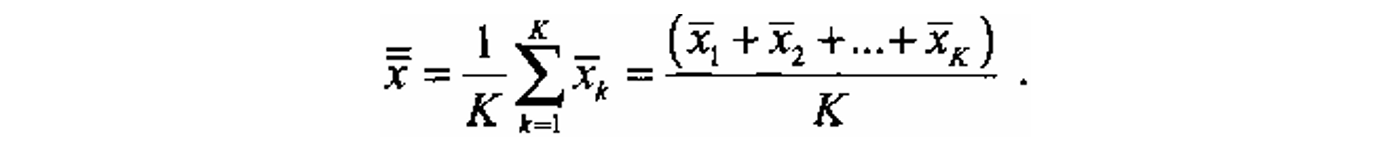
путем деления итога столбца xk на число подгрупп K.
Результат x надо вычислять с одним дополнительным знаком по сравнению с ранее вычисленными значениями xk (с двумя лишними знаками по сравнению с измеренными значениями х1, х2, ..., хn).
Примечание. Приведенные в табл. 3.7 данные содержат пять подгрупп, что соответствует K = 5. - Вычисление размаха Rk в каждой подгруппе путем вычитания минимального значения в подгруппе из максимального
Rk = xmax − xmin.
- Вычисление среднего арифметического значения размахов R для всех подгрупп данных
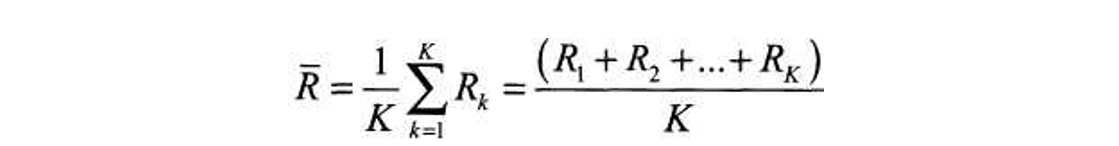
путем деления итога столбца размахов Rk для всех подгрупп на их число K. Этот результат надо вычислять с двумя лишними знаками по сравнению с измеренными значениями х1, х2, ..., хn. - Вычисление контрольных линий.
Вычислите значения, характеризующие положение каждой контрольной линии для x-карты и для R-карты по следующим формулам:
x-карта – Центральная линия (Central Line) CL = x.
Верхний контрольный предел (Upper Control Limit) UCL = x + A2R.
Нижний контрольный предел (Lower Control Limit) LCL = x − A2R.R-карта – Центральная линия CL = R.
Верхний контрольный предел (уровень) UCL = D4R.
Нижний контрольный предел (уровень) LCL = D3R.
Нижний предел не рассматривается, когда n < 7.Константы A2, D4, D3 – коэффициенты, определяемые объемом подгрупп n, приведены в табл. 3.8, заимствованной из [37].
Таблица 3.8
Коэффициенты для вычисления контрольных линий x-карт и R-карт [37]Объем подгруппы, n A2 D3 D4 d2 2 1,880 – 3,267 1,128 3 1,023 – 2,575 1,693 4 0,729 – 2,282 2,059 5 0,577 – 2,115 2,326 6 0,483 – 2,004 2,534 7 0,419 0,076 1,924 2,704 8 0,373 0,136 1,864 2,847 9 0,337 0,184 1,816 2,970 10 0,308 0,223 1,777 3,078 Нанесение контрольных линий.
Приготовьте лист бумаги в клеточку, затем нанесите слева вертикальные оси со значениями x и R и горизонтальные оси с номерами подгрупп. Разметьте верхний USL и нижний LSL пределы так, чтобы между ними оказалось 30–50 мм. Центральную линию CL начертите сплошной линией, а контрольные пределы – пунктирными линиями. Нанесите также на x-карту (жирными сплошными линиями) значения верхней USL и нижней LSL границ поля допуска (если эти значения USL и LSL имеются).
- Нанесение точек.
Выберите и разметьте масштабы по осям x и R, а по каждой горизонтальной оси нанесите номера подгрупп с небольшим интервалом 2–5 мм. Для удобства дальнейшего одновременного использования x-карты и R-карты можно рекомендовать нанесение тонких вертикальных линий для обозначения границ интервалов каждой подгруппы, причем эти тонкие линии должны проходить непрерывно через всю (x–R)-карту, так, как это показано на рис. 3.12.
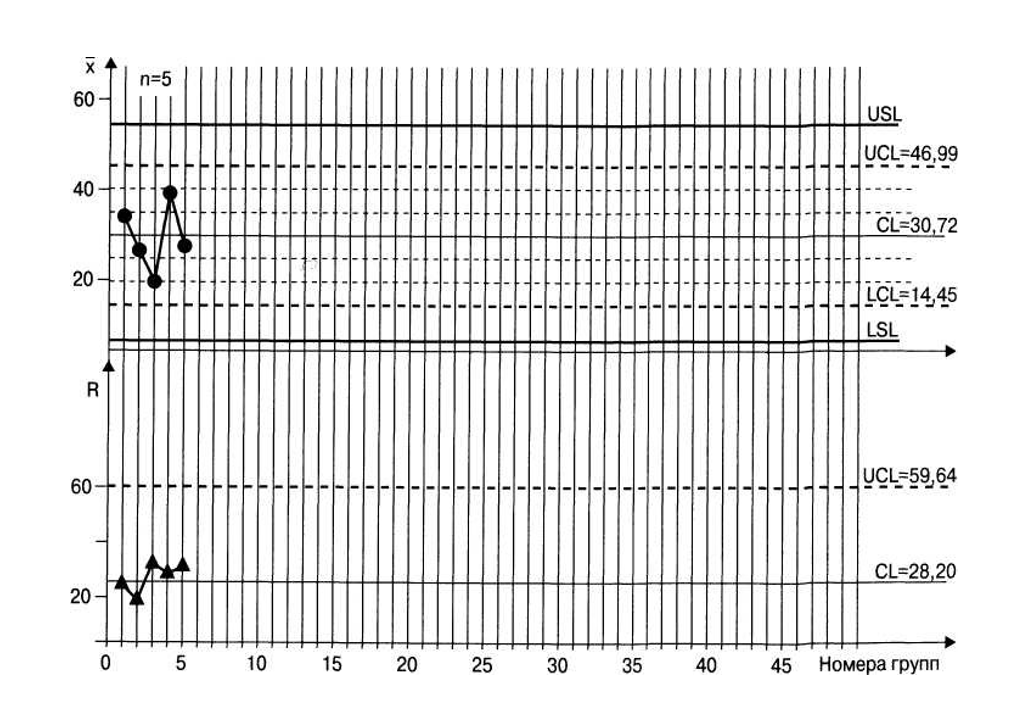
Рис. 3.12. Форма бланка (x–R)-карты
Чтобы легче было различать x и R, возьмем для изображения x один вид значка (например, точку), а для R – другой (например, крестик), а для тех значений, которые выходят за пределы контрольных линий, – кружочки. - Запишите необходимую информацию, например, объем подгрупп (n = 5) в верхнем левом углу x-карты. Запишите также и другие необходимые сведения, имеющие отношение к изучаемому процессу, такие как название процесса и продукции, период времени ведения контрольной карты, метод измерения, условия работы, смена, сведения о рабочем и т.п.
Внимание! На этом процесс подготовки формы (бланка) контрольной карты заканчивается.
Рассмотрим пример построения контрольной карты с использованием данных, приведенных в табл. 3.7.
Из таблицы видно, что для первой подгруппы
x1 = (47+32+44+35+20)/5 = 35,6;
R = 47−20 = 27.
Выполнив аналогичные подсчеты для других подгрупп, вычислим:
сначала
x = (35,6+29,2+20,2+39,4+29,2)/5 = 30,72;
R = (27+18+33+30+33)/5 = 28,2,
а затем определим для x-карты
CL = x = 30,72;
UCL = x + А2R¯= 30,72 + (0,577 × 28,2) = 46,99;
LCL = x − А2R¯ = 30,72 − (0,577 × 28,2) = 14,45
и для R-карты
CL = R = 28,2;
UCL = D4R¯ = 2,115 × 28,2 = 59,64;
LCL = D3R¯ не рассматривается, так как n = 5 < 7.
Используя полученные данные, строим контрольную карту. Обратите внимание, что интервалы (UCL – CL) и (CL – LCL) следует разделить на три равные части, например, так, как это показано на рис. 3.12.
3.7.4. Использование контрольных карт при контроле и регулировании процессов
Что важнее всего в процессе управления, так это точное понимание положения объекта управления с помощью чтения контрольной карты и быстрое осуществление подходящих действий, как только в объекте обнаружится что-нибудь необычное [45]. Контролируемое состояние объекта – это такое состояние, когда процесс стабилен, а его среднее значение x и разброс данных (размах R) не меняются (остаются близкими к x и R¯, т.е. не выходят за пределы верхнего UCL и нижнего LCL контрольных уровней). Находится ли процесс в контролируемом состоянии или нет, определяется по контрольной карте, на основании которой осуществляется либо простой контроль без вмешательства в ход процесса (когда процесс идет успешно), либо воздействие на процесс (его регулирование) при отклонении условий протекания процесса от нормальных.
Одной из предпочтительных рекомендаций оператору, осуществляющему управление процессом с использованием контрольной карты, может быть следующая: «Не дергайся понапрасну, не вмешивайся в ход процесса без достаточных на то оснований». Дело в том, что во многих случаях неопытные операторы, увидев незначительное отклонение хода процесса от центральной линии CL, стараются «улучшить» ход процесса. На самом деле эти действия (существует жаргонный термин – попытки «пощипать» процесс) приводят к резкому ухудшению качества процесса (с точки зрения теории автоматического управления происходит «раскачивание» процесса, что увеличивает отклонения x и R от центральных линий). В теории управления качеством операторам рекомендуется осуществлять вмешательство в ход процесса только при появлении на контрольной карте следующих сигнальных признаков [9, 39, 40, 45], проиллюстрированных на рис. 3.13.
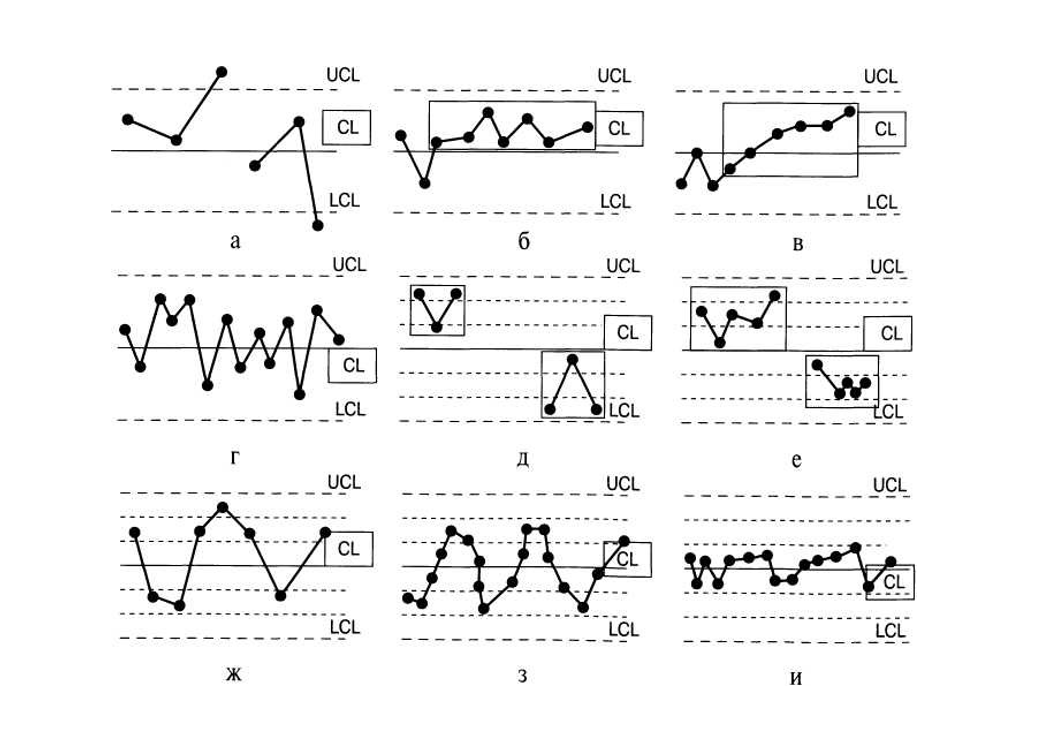
- Одна или более точек оказались за верхним или нижним контрольными пределами (рис. 3.13а).
- Серия из семи или более точек сразу оказалась с одной стороны от центральной линии (рис. 3.13б).
В данном случае под серией понимается проявление такого состояния процесса, когда ряд точек неизменно оказывается по одну сторону от средней линии. Серия длиной в семь точек рассматривается как ненормальная.
Примечание. Даже если длина серии оказывается менее семи или даже менее шести точек, в ряде случаев ситуацию следует рассматривать как ненормальную, например, когда:
а) не менее 10 из 11 точек оказываются по одну сторону от центральной линии; б) не менее 12 из 14 точек оказываются по одну сторону от центральной линии; в) не менее 16 из 20 точек оказываются по одну сторону от центральной линии. - Шесть или более точек подряд образуют ряд непрерывно возрастающих (убывающих) значений (рис. 3.13в).
Если точки образуют непрерывно повышающуюся или понижающуюся кривую, говорят, что имеет место тренд (дрейф). Это сигнализирует о ненормальности технологического процесса (изменение характеристики качества процесса происходит не из-за случайных вариаций условий протекания процесса, а из-за проявления неслучайной (специальной) причины, приводящей к изменению условий протекания процесса). Например, при обработке детали на токарном станке появление тренда (дрейфа) может быть вызвано повышенным износом резца. При этом оператор должен заменить резец на новый, чтобы не допустить выход характеристики качества процесса за контрольные пределы LCL или UCL.
- Четырнадцать точек скачут вверх-вниз (рис. 3.13г).
При работе на токарном станке этот сигнальный признак может свидетельствовать о том, что ослабло крепление резца. Оператор должен проверить это предположение и при необходимости закрепить инструмент.
- Две из трех точек подряд оказались в крайней трети диапазона контрольных пределов (приближение к контрольным пределам UCL и LCL) (рис. 3.13д).
Рассматриваются точки, которые располагаются в крайних трехсигмовых зонах контрольных пределов, причем если две из трех точек оказываются за двухсигмовыми линиями, то такой случай надо рассматривать как ненормальный, требующий анализа и вмешательства в ход процесса.
- Четыре из последовательных пяти точек находятся с одной стороны от центральной линии и не попадают в центральную треть диапазона контрольных пределов (рис. 3.13е). Оператору совместно с технологом следует выяснить причины такой ненормальной ситуации и принять меры для их устранения.
- Восемь точек расположены с двух сторон от средней линии, ни одна из которых не попадает в центральную треть диапазона контрольных пределов (рис. 3.13ж).
Оператору следует самостоятельно или с помощью инженера-технолога найти и устранить ненормальное протекание процесса.
- Периодичность изменения контролируемой характеристики качества процесса (рис. 3.13з).
Если точки укладываются на кривую, имеющую повторяющуюся форму (структуру) «то подъем, то спад» с примерно одинаковыми интервалами (периодами) времени, это тоже ненормально. Оператору и технологу следует найти и устранить причины этой ненормальности.
- Пятнадцать точек подряд оказались в пределах центральной трети диапазона контрольных пределов (рис. 3.13и).
При проведении занятий со студентами или с инженерами промышленных предприятий после формулирования этого сигнального признака преподаватели часто задают вопрос: «Что в этом случае надо делать?» Наиболее часто поступают ответы, сводящиеся к следующему: «Делать ничего не надо, так как процесс идет хорошо».
Японские и западноевропейские специалисты по качеству с этим не согласны. Они считают, что в этой ситуации нельзя бездействовать. Оператору необходимо срочно пригласить инженеров-технологов, так как в этот промежуток времени сложились очень благоприятные условия для проведения процесса. Эти условия следует зафиксировать, а затем превратить в нормативные (стандартные) условия осуществления этого процесса в будущем.
После этого придется пересчитать уменьшившееся среднее значение размахов R и, возможно, изменившееся значение x. Затем следует определить новые значения контрольных пределов UCL, LCL и подготовить новую форму контрольной карты, с помощью которой будет осуществляться дальнейший контроль и регулирование процесса.
Примечание. По мнению авторов книги [45], приближение большинства точек к центральной линии иногда может не означать, что достигнуто контролируемое состояние процесса. Напротив, если точки лежат в пределах полутора третей диапазона контрольных пределов, напримерCL − 1/2(CL − LCL) < X < CL + 1/2(UCL − CL),
то это может быть следствием того, что в подгруппах смешиваются данные из различных распределений, что делает размах контрольных пределов (UCL – LCL) слишком широким. В этом случае следует [45] изменить способ разбиения на подгруппы.
Источники:
- Васин С.Г. Управление качеством. Всеобщий подход : учебник для бакалавриата и магистратуры / С.Г. Васин. – М. : Издательство Юрайт, 2016.
- Гродзенский С.Я. Управление качеством : учебник. – Москва : Проспект, 2017.
- Пономарев С.В., Мищенко С.В., Белобрагин B.Я. и др. Управление качеством продукции. Инструменты и методы менеджмента качества: учебное пособие / С.В. Пономарев, С.В. Мищенко, B.Я. Белобрагин, В.А. Самородов, Б.И. Герасимов, А.В. Трофимов, C.А. Пахомова, О.С. Пономарева. – М.: РИА «Стандарты и качество». – 2005.